EL PRIMER TEOREMA DE THALES

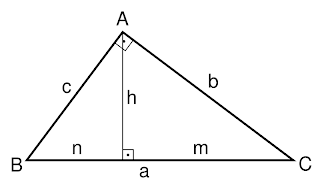
Es decir, que la igualdad de los cocientes equivale al paralelismo. Este teorema establece así una relación entre el álgebra y la geometría.
La primera figura corresponde a medidas algebraicas positivas - los vectores OA, OA', OB y OB' tienen la misma orientación que la rectas (d) y (d'), y la segunda a cocientes negativos.
Si se aplica el teorema, tenemos además otra consecuencia: si se orienta de la misma manera las dos rectas paralelas (AB) y (A'B'), es decir con el mismo vector, entonces el tercer cociente (de medidas algebraicas): A'B' / AB es igual a los dos anteriores.
A veces se reserva el nombre de teorema de Tales al sentido directo de la equivalencia, y el otro sentido recibe el nombre de recíproca del teorema de Tales.
Este teorema es un caso particular de los triángulos similares o semejantes.

Una aplicación del Teorema de Tales
Una aplicación interesante es para medir la altura de un árbol.
Medimos la longitud de su sombra a una hora determinada. = C
Medimos la longitud de la sombra de un objeto pequeño (por ejemplo un lápiz) en el mismo instante. = B
Medimos la longitud real del mismo cuerpo. = A
Y obtenemos donde D es la altura real del árbol.
También se puede relacionar para medir una distancia, cuya finidad no pueda ser medida, y apoyándose en un punto.

TEOREMA DE THALES

El teorema de Tales demuestra la relación de proporcionalidad entre los segmentos que delimitan rectas secantes sobre rectas paralelas. Es muy útil para dividir un segmento en partes iguales o proporcionales a otros segmentos.

Se estima que se demostró el teorema mediante semejanza de triángulos: sus lados homólogos son proporcionales.[1]
Sea el triángulo ABC, rectángulo en C. El segmento CH es la altura relativa a la hipotenusa, en la que determina los segmentos a’ y b’, proyecciones en ella de los catetos a y b, respectivamente.
Los triángulos rectángulos ABC, AHC y BHC tienen sus tres bases iguales: todos tienen dos bases en común, y los ángulos agudos son iguales bien por ser comunes, bien por tener sus lados perpendiculares. En consecuencia dichos triángulos son semejantes.
De la semejanza entre ABC y AHC:
Los resultados obtenidos son el teorema del cateto. Sumando:
Pero , por lo que finalmente resulta:
La relación entre las superficies de dos figuras semejantes es igual al cuadrado de su razón de semejanza. En esto pudo haberse basado Pitágoras para demostrar su teorema
Pitágoras también pudo haber demostrado el teorema basándose en la relación entre las superficies de figuras semejantes.
Los triángulos PQR y PST son semejantes, de manera que:
siendo r la razón de semejanza entre dichos triángulos. Si ahora buscamos la relación entre sus superficies:
obtenemos después de simplificar que:
pero siendo la razón de semejanza, está claro que:
Es decir, "la relación entre las superficies de dos figuras semejantes es igual al cuadrado de la razón de semejanza".
Aplicando ese principio a los triángulos rectángulos semejantes ACH y BCH tenemos que:
que de acuerdo con las propiedades de las proporciones nos da:
(I)
y por la semejanza entre los triángulos ACH y ABC resulta que:
Pero según (I) , así que:
y por lo tanto:
Quedando demostrado el teorema de Pitágoras.
Los cuadrados compuestos en el centro y a la derecha tienen áreas equivalentes. Quitándoles los triángulos el teorema de Pitágoras queda demostrado.
Es asimismo posible que Pitágoras hubiera obtenido una demostración gráfica del teorema.
Partiendo de la configuración inicial, con el triángulo rectángulo de lados a, b, c, y los cuadrados correspondientes a catetos e hipotenusa –izquierda-, se construyen dos cuadrados iguales:
Uno de ellos –centro- está formado por los cuadrados de los catetos, más cuatro triángulos rectángulos iguales al triángulo inicial.
El otro cuadrado –derecha- lo conforman los mismos cuatro triángulos, y el cuadrado de la hipotenusa.
Si a cada uno de estos cuadrados les quitamos los triángulos, evidentemente el área del cuadrado gris (c2) equivale a la de los cuadrados amarillo y azul (b2 + a2), habiéndose demostrado el teorema de Pitágoras.

PROPIEDADES DE LA HIPOTENUSA

El cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos.
a² = b² + c²

Proyecciones ortogonales:
La longitud de la hipotenusa es igual a la suma de las longitudes de las proyecciones ortogonales de ambos catetos.
El cuadrado de la longitud de un cateto es igual al producto de la longitud de su proyección ortogonal sobre la hipotenusa por la longitud de ésta.
b² = a · m
c² = a · n
También, la longitud de un cateto b es media proporcional entre las longitudes de su proyección m y la de la hipotenusa a.
a/b = b/m
a/c = c/n
En la figura, la hipotenusa es el lado a y los catetos son los lados b y c. La proyección ortogonal de b es m, y la de c es n.

LAS RAZONES TRIGONOMETRICAS

Mediante razones trigonométricas se puede obtener el valor de los dos ángulos agudos, y , del triángulo rectángulo.
Conocida la longitud de la hipotenusa y la de un cateto , la razón entre ambos es:


Por tanto, la función trigonométrica inversa es:

Siendo el valor del ángulo opuesto al cateto .
El ángulo contiguo al cateto , será = 90º –
También se puede obtener el valor del ángulo mediante la ecuación:

Siendo el otro cateto.

CUANTOS TIPOS DE GEOMETRIA HAY!!!

Entre los más sobre salientes se encuentran:

1- La geometría euclidea.

2- La geometría analítica.

3- La geometría hiperbólica

.
4- La geometría proyectiva.

5-La geometría elíptica.

¿QUE ES LA GEOMETRIA?

La geometría es una rama de las matemáticas que se ocupa de las propiedades del espacio, como son: puntos, rectas, planos, polígonos, poliedros, curvas, superficies, etc. Se utiliza para solucionar problemas concretos y es la justificación teórica de muchos instrumentos, por ejemplo el compás, el teodolito y el pantógrafo.
Así mismo, da fundamento teórico a inventos como el sistema de posicionamiento global (en especial cuando se la considera en combinación con el análisis matemático y sobre todo con las ecuaciones diferenciales) y es útil en la preparación de diseños (justificación teórica de la geometría descriptiva, del dibujo técnico e incluso en la fabricación de artesanías).

La historia del origen de la Geometría es muy similar a la de la Aritmética, siendo sus conceptos más antiguos consecuencia de las actividades prácticas. Los primeros hombres llegaron a formas geométricas a partir de la observación de la naturaleza.El sabio griego Eudemo de Rodas, atribuyó a los egipcios el descubrimiento de la geometría, ya que, según él, necesitaban medir constantemente sus tierras debido a que las inundaciones del Nilo borraban continuamente sus fronteras. Recordemos que, precisamente, la palabra geometría significa medida de tierras.

Los egipcios se centraron principalmente en el cálculo de áreas y volúmenes, encontrando, por ejemplo, para el área del círculo un valor aproximado de ( de 3'1605. Sin embargo el desarrollo geométrico adolece de falta de teoremas y demostraciones formales. También encontramos rudimentos de trigonometría y nociones básicas de semejanza de triángulos.

También se tienen nociones geométricas en la civilización mesopotámica, constituyendo los problemas de medida el bloque central en este campo: área del cuadrado, del círculo (con una no muy buena aproximación de (=3), volúmenes de determinados cuerpos, semejanza de figuras, e incluso hay autores que afirman que esta civilización conocía el teorema de Pitágoras aplicado a problemas particulares, aunque no, obviamente, como principio general.

No se puede decir que la geometría fuese el punto fuerte de las culturas china e india, limitándose principalmente a la resolución de problemas sobre distancias y semejanzas de cuerpos. También hay quien afirma que estas dos civilizaciones llegaron a enunciados de algunos casos particulares del teorema de Pitágoras, e incluso que desarrollaron algunas ideas sobre la demostración de este teorema.